最小凸包 | 玉书

2021-06-18

问题描述

求点集的最小凸包

平面上有3个及以上的点, 求这些点的最小外接凸多边形(凸包)

演示

生成最小凸包重置生成随机点

前置知识

参考链接

方法介绍

穷举法 (O(n³))

穷举法试图枚举出所有可能, 并从中找到满足要求的情况. 所以重点是找到凸包顶点的充要条件, 这里判断的依据是:

若AB之外的点都在直线 $\overline{AB}$ 的同一侧, 则点A和点B都是凸包的顶点

计算的步骤为:

从点集里取出一点A, 与剩下的点B依次连接, 得到一条直线L( $\overline{AB}$ ) (共 $\displaystyle\sum_{i=1}^{n-1}{i}$ 条)
判断其他点(共 $n - 2$ 个)是否都在直线L的同一侧, 是则将L加入边数组
[按需] 将边数组转换为点数组 (将边首尾相连并展平O(n㏒n))

演示

生成最小凸包重置加速减速生成随机点

推导及代码实现

import type { Point, Algorithm } from './types'

/** 穷举法求最小凸包 */
const exhaust: Algorithm = function* (points: Point[]) {
  const size = points.length
  if (size < 4) {
    return points
  }

  const result: Point[][] = []

  let i = size
  while (i) {
    const p0 = points[--i]
    const { x, y } = p0
    let j = i
    while (j) {
      // 线段 [p0, p1]
      const p1 = points[--j]

      const dx = p1.x - x
      const dy = p1.y - y

      let lastTurn: boolean | null = null

      let k = size
      while (k) {
        if (--k === i || k === j) {
          continue
        }
        // 检查其他点是否在线段所在直线的同一侧
        const p2 = points[k]

        yield result.concat([[p0, p1, p2]])

        const turn = dx * (p2.y - y) > (p2.x - x) * dy
        if (lastTurn === null) {
          lastTurn = turn
        } else if (turn !== lastTurn) {
          lastTurn = null
          break
        }
      }

      if (lastTurn !== null) {
        result.push([p0, p1])
        yield result
      }
    }
  }

  return result
}

export default exhaust

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

分治法 (快包 O(n㏒n))

也叫快速凸包构造算法(快包), 核心思想(分而治之)为:

划分点集为更小的点集, 直到能解决问题, 然后汇总结果

对于一个点集, 最容易确定是凸包顶点的, 是上下左右4个极值点(集)(x/y有相等时取两端参与划分), 剩下的点集暂时无法确定

基于这4个极值点(集), 可以想到把点集划分为5个区域, 很明显在中间的4-8边形内不可能存在凸包顶点, 剩余的4个区域(左上角、右上角、左下角、右下角) 可能存在凸包顶点

这4个区域可以视作新的点集继续划分, 但是问题是: 新的点集的极值点就不一定是凸包顶点了(请自己尝试)

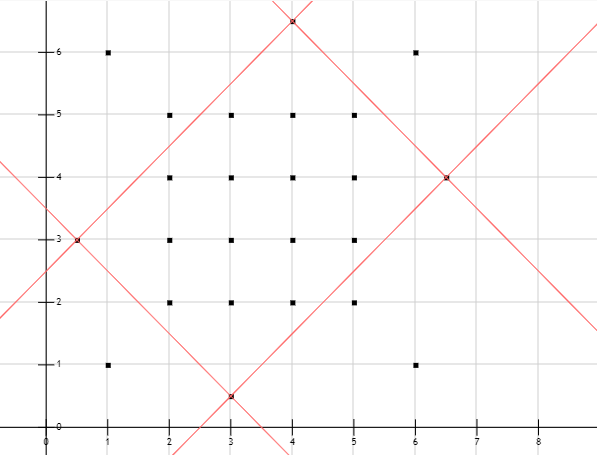
我们需要用别的方式找到凸包上的点, 很容易证明:

到划分线距离最远的点一定是凸包上的点

^{划分线即凸包顶点的连线, 比如前面提到的极值点, 这里用于将点集进行划分}

所以考虑将划分方式改为三角形, 整理下计算的步骤:

找到x极值点p0和p1(p0.x < p1.x>), 线段 $\overline{p_0p_1}$ 将点集划分为两个部分, 称作上包(逆时针方向)和下包(顺时针方向)
在上包中找到离直线 $\overline{p_0p_1}$ $\overline{p_{0} p_{1}}$ 最远的点p2, 分别使用直线 $\overline{p_0p_2}$ $\overline{p_{0} p_{2}}$ 和直线 $\overline{p_2p_1}$ $\overline{p_{2} p_{1}}$ 继续划分出新的上包A(逆时针方向, 下包一定在多边形内部了)
1. 若A为空, 不再继续划分
2. A不为空则对A按照步骤2进行划分
对下包也做与第2步相似的操作

演示

生成最小凸包重置加速减速生成随机点

推导及代码实现

使用前置知识中介绍过的通过叉积的正负判断点在线段的顺时针/逆时针方向的方法, 叉积的绝对值表示两向量围成的平行四边形面积, 距离最远的点一定可以围出最大的面积(底相等, 高越大面积越大), 据此可以划分上下包及找到距离划分线最远的点

import type { Point, Algorithm } from './types'

function* cut(
  points: Point[],
  start: Point,
  middle: Point,
  end: Point,
  result: Point[] // 需要画出来 故
): Generator<Point[], Point[]> {
  // 按顺时针算使叉积为正
  const { x: startX, y: startY } = start
  const startMiddleDx = middle.x - startX
  const startMiddleDy = middle.y - startY
  const startMiddlePoints: Point[] = [] // middleStart顺时针方向 点集
  let startMiddleMax = 0 // middleStart顺时针方向 最大距离 +
  let startMiddle!: Point // middleStart顺时针方向 距离最远点

  const { x: middleX, y: middleY } = middle
  const middleEndDx = end.x - middleX
  const middleEndDy = end.y - middleY
  const middleEndPoints: Point[] = [] // endMiddle顺时针方向 点集
  let middleEndMax = 0 // endMiddle顺时针方向 最大距离 +
  let middleEnd!: Point // endMiddle顺时针方向 距离最远点

  let point: Point
  let area: number
  let i = points.length
  while (i) {
    point = points[--i]

    area = startMiddleDx * (point.y - startY) - (point.x - startX) * startMiddleDy
    if (area > 0) {
      yield result.concat(middle, point)
      startMiddlePoints.push(point)
      if (area > startMiddleMax) {
        startMiddleMax = area
        startMiddle = point
      }
    } else {
      area = middleEndDx * (point.y - middleY) - (point.x - middleX) * middleEndDy
      if (area > 0) {
        yield result.concat(end, point)
        middleEndPoints.push(point)
        if (area > middleEndMax) {
          middleEndMax = area
          middleEnd = point
        }
      }
    }
  }

  if (startMiddle) {
    yield* cut(startMiddlePoints, start, startMiddle, middle, result)
  }
  result.push(middle)
  if (middleEnd) {
    yield* cut(middleEndPoints, middle, middleEnd, end, result)
  }

  return result
}

/** 分治法求最小凸包 使用canvas坐标系, 如下
o——→ x
|
↓
y
*/
const divide: Algorithm = function* (points) {
  const size = points.length
  if (size < 4) {
    return points
  }

  let left!: Point
  let right!: Point

  let point: Point
  let i = size
  while (i) {
    point = points[--i]

    if (!left || left.x > point.x) {
      left = point
    }

    if (!right || right.x < point.x) {
      right = point
    }
  }

  const { x, y } = left
  const dx = right.x - x
  const dy = right.y - y

  let max = 0 // 上包最大距离 +
  let min = 0 // 下包最大距离 -

  let top!: Point // 上包距离最远点
  let bottom!: Point // 下包距离最远点

  const up: Point[] = [] // 上包点集
  const down: Point[] = [] // 下包点集

  let area: number
  i = size
  while (i) {
    point = points[--i]
    yield [left, right, point]
    area = dx * (point.y - y) - (point.x - x) * dy

    if (area > 0) {
      up.push(point)
      if (area > max) {
        max = area
        top = point
      }
    } else if (area < 0) {
      down.push(point)
      if (area < min) {
        min = area
        bottom = point
      }
    }
  }

  if (left === right) {
    return [top, bottom]
  }
  if (top === bottom) {
    return [left, right]
  }

  const result: Point[] = [left] // 顺时针
  if (top) {
    yield* cut(up, left, top, right, result)
  }
  result.push(right)
  if (bottom) {
    yield* cut(down, right, bottom, left, result)
  }

  return result
}

export default divide

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146

Jarvis 步进法 (O(nH))

把点集想象成木板上钉的若干钉子, 要构造出最小凸包, 我们可以借助一根绳子, 先找到一颗最外面的钉子, 然后顺时针或逆时针绕着木板行走, 每次绳子将和一颗或多颗钉子同时接触, 走一圈下来即可围出最小凸包

计算的步骤为:

左上、右上、左下、右下四个角处的点一定是凸包上的点, 因此选任意一个用来作为起点
依次从剩下的点里取出一个点, 按照顺时针或逆时针方向, 夹角最接近平角的点(存在多个时任取一个就行)即为凸包顶点

优化一下:

先找到左上角的点入栈, 选取顺时针方向遍历, 结果为点数组(栈), 先将下一个非起点的点入栈
遍历全部点
1. 若一个点A在栈顶两点向量的逆时针方向则用点A替换栈顶继续下一个点
2. 若完成本轮遍历时得到的顶点为起点, 则结束, 否则入栈继续下一轮

演示

生成最小凸包重置加速减速生成随机点

推导及代码实现

import type { Point, Algorithm } from './types'

const isPointEqual = (a: Point, b: Point) => a === b || (a.x === b.x && a.y === b.y)

/** jarvis步进法求最小凸包 使用canvas坐标系, 如下
o——→ x
|
↓
y
*/
const jarvis: Algorithm = function* (points) {
  const size = points.length
  if (size < 4) {
    return points
  }

  let start!: Point

  let point: Point
  let i = size
  while (i) {
    point = points[--i]

    if (!start || point.x < start.x || (point.x === start.x && point.y < start.y)) {
      start = point
    }
  }

  const result: Point[] = [start]

  let pointer = 0 // 栈顶
  let startPoint: Point
  let x: number
  let y: number
  let dx: number
  let dy: number
  let j: number
  i = size
  while (i) {
    point = points[--i]
    startPoint = result[pointer]
    if (isPointEqual(point, startPoint)) {
      continue
    }

    result.push(point)
    pointer++

    x = startPoint.x
    y = startPoint.y
    dx = point.x - x
    dy = point.y - y

    j = size
    while (j) {
      point = points[--j]
      yield result.concat(point)

      if (dx * (point.y - y) < (point.x - x) * dy) {
        result[pointer] = point
        dx = point.x - x
        dy = point.y - y
      }
    }

    if (isPointEqual(result[pointer], start)) {
      result.pop()
      break
    }
  }

  return result
}

export default jarvis

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

Graham 扫描法 (O(n㏒n)) ^[1]

在Jarvis 步进法中, 我们已经可以顺时针或逆时针地将凸包围出来了, 但是每次都要去遍历所有的点判断其时针方向才能确定一个顶点, 那要是我们按照时针方向去一个个寻找顶点不就只需要遍历一次了么？

Graham 扫描法就是这个思路, 还是先找到一个起点, 然后剩下的点按照相对起点的时针方向排序, 然后进行连接

计算的步骤为(左上角起顺时针方向):

找到左上角点作为起点O
将点集按照与起点O的幅角(y轴正向)从小到大排序, 幅角相等则按与起点O的距离排序(近的在前), 先把第一个点添加进凸包顶点数组末尾
从排序数组中取出第一个点A, 直到数组为空时结束
从凸包数组取末尾两点得到一条直线L, 若点A在直线L顺时针方向, 则将点A加入凸包数组, 继续执行第3步; 否则移除凸包数组末尾点, 继续执行第4步

演示

生成最小凸包重置加速减速生成随机点

推导及代码实现

其他点与起点的幅角范围为 [0, 180°], 使用 $\cos$ 函数即可排序幅角, 同时可计算出距离

import type { Point, Algorithm } from './types'

const isPointEqual = (a: Point, b: Point) => a === b || (a.x === b.x && a.y === b.y)

/** 将 point 插入到 points 的 position 下标 (最多挪动一半元素)
 * @param points
 * @param point
 * @param position 整数范围: [0, points.length)
 */
export function insertAt(points: Point[], point: Point, position: number) {
  let pointer = points.length
  if (position < pointer >> 1) {
    points.unshift(points[0])
    pointer = 1
    while (pointer <= position) {
      points[pointer] = points[++pointer]
    }
  } else {
    while (pointer > position) {
      points[pointer] = points[--pointer]
    }
  }
  points[position] = point
}

/** [稳定] 将 point 插入 points
 * @param point
 * @param points
 * @param compare 比较方法 返回 true: element > point
 */
function insert(
  point: Point,
  points: Point[],
  compare: (element: Point, point: Point) => boolean
) {
  // 二分查找 [low, high]
  let low = 0
  let mid: number
  let high = points.length - 1
  while (low <= high) {
    mid = (low + high) >> 1 // 除2并向下取整
    if (compare(points[mid], point)) {
      high = mid - 1
    } else {
      low = mid + 1
    }
  }

  // points.splice(low, 0, point)
  insertAt(points, point, low)
}
/** 将点集按与 start→x轴正向 的幅角 排序 (幅角相等按距离)
 * @param points
 * @param start
 * @returns
 */
function sortPoints(points: Point[], start: Point) {
  const result: Point[] = []

  /** 缓存点与起点的角度、距离 */
  const cache = new WeakMap<Point, [/** angle */ number, /** distance */ number]>()
  const getInfo = (point: Point) => {
    let info = cache.get(point)
    if (!info) {
      const distance = ((start.x - point.x) ** 2 + (start.y - point.y) ** 2) ** 0.5
      info = [(point.y - start.y) / distance, distance]
      cache.set(point, info)
    }

    return info
  }

  const compare = (element: Point, point: Point) => {
    const elementInfo = getInfo(element)
    const pointInfo = getInfo(point)

    return elementInfo[0] === pointInfo[0]
      ? elementInfo[1] < pointInfo[1]
      : elementInfo[0] < pointInfo[0]
  }

  let i = points.length
  while (i) {
    isPointEqual(points[--i], start) || insert(points[i], result, compare)
  }

  return result
}

/** graham扫描法求最小凸包 使用canvas坐标系, 如下
o——→ x
|
↓
y
*/
const graham: Algorithm = function* (points) {
  let i = points.length
  if (i < 4) {
    return points
  }

  let start!: Point

  let point: Point
  while (i) {
    point = points[--i]

    if (!start || point.x < start.x || (point.x === start.x && point.y < start.y)) {
      start = point
    }
  }

  const result: Point[] = [start]

  let pointer = 1 // 栈顶
  let startPoint: Point
  let endPoint: Point
  points = sortPoints(points, start)
  i = points.length
  i && result.push(points[--i])
  yield result
  while (i) {
    point = points[i - 1]
    yield result.concat(point)

    startPoint = result[pointer - 1]
    endPoint = result[pointer]

    if (
      (endPoint.x - startPoint.x) * (point.y - startPoint.y) <
      (point.x - startPoint.x) * (endPoint.y - startPoint.y)
    ) {
      result.pop()
      pointer--
    } else {
      result.push(point)
      pointer++
      i--
    }
  }

  return result
}

export default graham

Melkman 算法 (O(n))

从Graham 扫描法改进而来, 改进的思路是: Graham 扫描法一次只能从一端处理下一个有序点, 若是可以打开合适的位置, 那么任意一点都可以成为"下一个有序点", 从而使用同样的方式去处理. 因此它也变成了一个在线算法: 在得到一个三角形凸包后, 之后每加入一个点就按上述思路对凸包进行调整. 该算法在输入的点有序时(按照幅角排序), 时间复杂度可达到O(n), 否则 O(n㏒n)

计算的步骤为:

先依次取出点, 直到能构造出顺时针方向的三角形 (注意可能存在三点共线的情况)
读取下一点A, 顺时针遍历凸包上的边
1. 若点A在所有边的顺时针方向, 则点A在凸包内部, 继续步骤2
2. 若点A在其中一条边L的逆时针方向, 则点A在凸包外部, 从边L处"打开"凸包, 使用与 Graham 扫描法相似的方法(步骤3)连接该点, 然后继续步骤2

演示

生成最小凸包重置加速减速生成随机点

推导及代码实现

import type { Point, Algorithm } from './types'
import { insertAt } from './graham'

const isPointEqual = (a: Point, b: Point) => a === b || (a.x === b.x && a.y === b.y)

function* insertVertex(convex: Point[], vertex: Point, position: number) {
  let pointer = convex.length

  insertAt(convex, vertex, position)
  yield convex.concat(convex[0])

  let middlePointer = position ? position - 1 : pointer
  let endPointer: number
  const startVertex = convex[position]
  let middleVertex = convex[middlePointer]
  let endVertex: Point
  while (middleVertex !== startVertex) {
    endPointer = middlePointer ? middlePointer - 1 : pointer
    endVertex = convex[endPointer]

    if (
      (middleVertex.x - startVertex.x) * (endVertex.y - startVertex.y) <=
      (endVertex.x - startVertex.x) * (middleVertex.y - startVertex.y)
    ) {
      break
    }

    convex.splice(middlePointer, 1) // 优化: 循环外面处理
    pointer--
    position && position--
    middlePointer = position ? position - 1 : pointer
    middleVertex = convex[middlePointer]
    yield convex.concat(convex[0])
  }

  const lastMiddleVertex = middleVertex
  middlePointer = position === pointer ? 0 : position + 1
  middleVertex = convex[middlePointer]
  while (middleVertex !== startVertex && middleVertex !== lastMiddleVertex) {
    endPointer = middlePointer === pointer ? 0 : middlePointer + 1
    endVertex = convex[endPointer]

    if (
      (middleVertex.x - startVertex.x) * (endVertex.y - startVertex.y) >=
      (endVertex.x - startVertex.x) * (middleVertex.y - startVertex.y)
    ) {
      break
    }

    convex.splice(middlePointer, 1) // 优化: 循环外面处理
    pointer--
    middlePointer = middlePointer === pointer ? 0 : middlePointer
    middleVertex = convex[middlePointer]
    yield convex.concat(convex[0])
  }

  return pointer
}

/** melkman算法法求最小凸包 使用canvas坐标系, 如下
o——→ x
|
↓
y
*/
const melkman: Algorithm = function* (points) {
  let i = points.length
  if (i < 4) {
    return points
  }

  const result: Point[] = [points[--i]]

  let pointer = 0 // 栈顶
  let startPoint: Point
  let endPoint: Point

  let point: Point
  let product: number
  // 构造初始凸包(三角形)
  while (i) {
    point = points[--i]
    endPoint = result[pointer]
    if (isPointEqual(point, endPoint)) {
      continue
    }
    yield result.concat(point, result[0])

    startPoint = result[pointer - 1]
    if (!startPoint) {
      result.push(point)
      pointer++
      continue
    }

    product =
      (endPoint.x - startPoint.x) * (point.y - startPoint.y) -
      (point.x - startPoint.x) * (endPoint.y - startPoint.y)
    if (!product) {
      // 共线 只保留两端的点叭~
      if (
        (point.x < startPoint.x && point.x < endPoint.x) ||
        (point.y < startPoint.y && point.y < endPoint.y)
      ) {
        result[startPoint.x < endPoint.x || startPoint.y < endPoint.y ? pointer - 1 : pointer] =
          point
      } else if (
        (point.x > startPoint.x && point.x > endPoint.x) ||
        (point.y > startPoint.y && point.y > endPoint.y)
      ) {
        result[startPoint.x > endPoint.x || startPoint.y > endPoint.y ? pointer - 1 : pointer] =
          point
      }
      continue
    }

    // 保证三个点顺时针方向
    if (product > 0) {
      result.push(point)
    } else {
      result[2] = result[1]
      result[1] = point
    }
    pointer++
    break
  }

  // 依次连接下一个点
  let startPointer: number
  let endPointer: number
  while (i) {
    point = points[--i]
    yield result.concat(point, result[0])

    for (startPointer = 0, endPointer = pointer + 1; endPointer--; startPointer = endPointer) {
      startPoint = result[startPointer]
      endPoint = result[endPointer]

      if (
        (endPoint.x - startPoint.x) * (point.y - startPoint.y) >=
        (point.x - startPoint.x) * (endPoint.y - startPoint.y)
      ) {
        // 点在当前凸包外面
        pointer = yield* insertVertex(result, point, startPointer)
        break
      }
    }
  }

  return result
}

export default melkman

升维

3D中的情况如何?

凸包问题——快速凸包算法

参考链接

凸包算法剖析

Understanding Graham scan algorithm for finding the Convex hull of a set of Points ↩︎

算法

点是否在多边形内

# 问题描述

# 演示

# 前置知识

# 方法介绍

# 穷举法 (O(n3))

# 演示

# 分治法 (快包 O(n㏒n))

# 演示

# Jarvis 步进法 (O(nH))

# 演示

# Graham 扫描法 (O(n㏒n)) [1]

# 演示

# Melkman 算法 (O(n))

# 演示

# 升维

# 参考链接

问题描述

演示

前置知识

方法介绍

穷举法 (O(n³))

演示

分治法 (快包 O(n㏒n))

演示

Jarvis 步进法 (O(nH))

演示

Graham 扫描法 (O(n㏒n)) ^[1]

演示

Melkman 算法 (O(n))

演示

升维

参考链接